排序算法及其比较

文章目录

1. 冒泡排序
2. 选择排序
3. 插入排序
4. 希尔排序
5. 归并排序
6. 快速排序
7. 堆排序
8. 排序算法的比较
9. 参考：

这里以从小到大排序为例

冒泡排序

steps：

比较相邻的元素，将较大的交换到右边

从0~n-1重复相同的工作，n-1次比较后最大数冒到了最右边(即n-1的位置)

同理将第二大数冒泡到n-2位，以此类推就完成了冒泡排序

动态演示：

c代码：

void Swap(int *a,int *b)
{
	int tmp;
	tmp = *a;
	*a = *b;
	*b = tmp;
}

/*冒泡排序*/
void BubbleSort(int a[],int n)
{
	int i,j;
	for (i=0;i<n;i++)
	{
		for (j=1;j<n-i;j++)
		{
			if (a[j-1] > a[j])
			{
				Swap(&a[j-1],&a[j]);
			}
		}
	}
}

两种优化方案

某次遍历若无数据交换，则说明已排序好了，无序进行接下来的操作了。

void BubbleSort2(int a[],int n)
{
	int i,k;
	bool flag;

	k =n;
	flag = true;
	while(flag)
	{
		flag = false;
		for (i=1;i<k;i++)
		{
			if (a[i-1] > a[i])
			{
				Swap(&a[i-1],&a[i]);
				flag = true;
			}
		}
		k--;
	}
}

记录某次遍历最后发生交换的位置，这个位置之后的数据已经排序好了，无序再排。

void BubbleSort3(int a[],int n)
{
	int i,k;
	int flag;

	flag = n;
	while(flag >0)
	{
		k = flag;
		flag = 0;
		for (i=1;i<k;i++)
		{
			if (a[i-1] > a[i])
			{
				Swap(&a[i-1],&a[i]);
				flag = i;
			}
		}
	}
}

选择排序

steps

在未排序的序列中找到最小的元素，存放到未排序序列的起始位置

接下来对剩下未排序的队列进行step1操作

以此类推，直到所有元素排序完毕

动态演示：

c代码：

/*选择排序*/
void SelectSort(int a[],int n)
{
	int i,j,min;

	for (i=0;i<n;i++)
	{
		min = a[i];
		for (j=i;j<n;j++)
		{
			if (a[j]<min)
			{
				min = a[j];
			}
		}
		a[i] = min;
	}
}

插入排序

排序演示：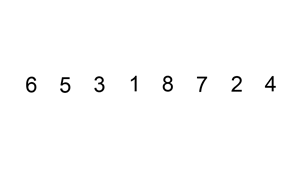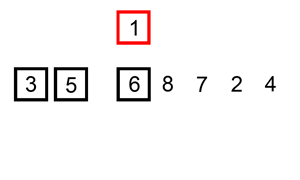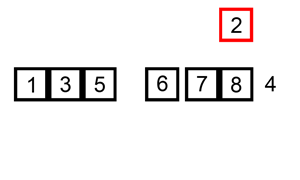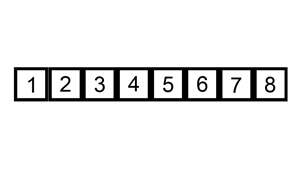
insertsort

c代码：

/*插入排序*/
void InsertSort(int a[],int n)
{
	int i,j;
	for (i=1;i<n;i++)
	{
		for (j=i-1;j>=0 && a[j]>a[j+1];j--)
		{
			Swap(&a[j],&a[j+1]);
		}
	}
}

希尔排序

也称递减增量排序算法，实质是分组插入排序。
wikipedia上的解释
演示图

/*希尔排序*/
void ShellSort(int a[],int n)
{
	int i,j,gap;

	for (gap=n/2;gap>0;gap/=2)
	{
		for (i=gap;i<n;i++)
		{
			for (j=i-gap;j>=0 && a[j]>a[j+gap];j-=gap)
			{
				Swap(&a[j],&a[j+gap]);
			}
		}
	}
}

归并排序

该算法采用分治法的一个非常经典的引用，且各层分治递归可以同时进行。

归并排序演示：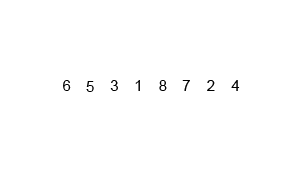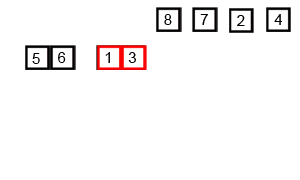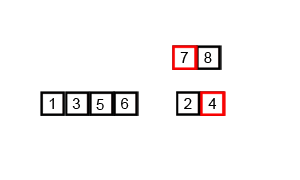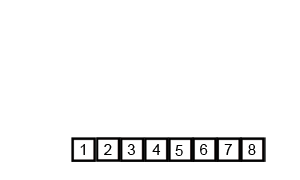

总体思想：先分再和

c代码：

//将有二个有序数列a[first...mid]和a[mid+1...last]合并。
void mergearray(int a[], int first, int mid, int last, int temp[])
{
	int i = first, j = mid + 1;
	int m = mid,   n = last;
	int k = 0;
	
	while (i <= m && j <= n)
	{
		if (a[i] <= a[j])
			temp[k++] = a[i++];
		else
			temp[k++] = a[j++];
	}
	
	while (i <= m)
		temp[k++] = a[i++];
	
	while (j <= n)
		temp[k++] = a[j++];
	
	for (i = 0; i < k; i++)
		a[first + i] = temp[i];
}
void mergesort(int a[], int first, int last, int temp[])
{
	if (first < last)
	{
		int mid = (first + last) / 2;
		mergesort(a, first, mid, temp);    //左边有序
		mergesort(a, mid + 1, last, temp); //右边有序
		mergearray(a, first, mid, last, temp); //再将二个有序数列合并
	}
}

bool MergeSort(int a[], int n)
{
	int *p = new int[n];
	if (p == NULL)
		return false;
	mergesort(a, 0, n - 1, p);
	delete[] p;
	return true;
}

快速排序

快速排序算法通常情况下明显比同为Ο(nlogn)复杂度的其它算法快，因此使用较多。排序中使用了分治法思想。

stes:

确定基数，即从队列中挑选出一个元素

以基数为基准将队列一分为二，即将小于基数的元素放在队列左侧，而大于基数的元素放在队列右侧

在对基数的左右两个队列分别进行上述操作，直至各区间只剩下一个元素为止

动态演示：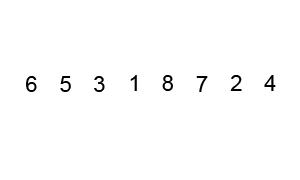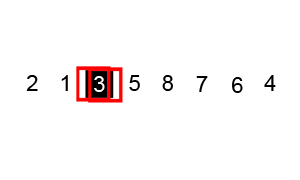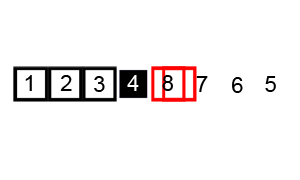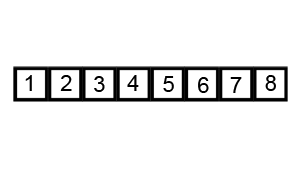

c代码：

void QuickSort(int input[], int begin, int end)
{
	int i,j;

	if (begin >= end)
	{
		return;
	}

	//key = input[end];
	//Swap(&input[k],&input[end]);
	
	i = begin-1;
	j = end;

	while (1)
	{
		do 
		{
			i++;
		} while (input[i]>input[end]);

		do 
		{
			j--;
		} while (input[j]<input[end]);

		if (i<j)
		{
			Swap(&input[i],&input[j]);
		}else{
			break;
		}
		
	}

	Swap(&input[end], &input[i]);
	QuickSort(input,begin,j-1);
	QuickSort(input,j+1,end);
}

堆排序

堆排序中使用了二叉堆的概念

二叉堆通常通过一维数组表示，若起始数组为0，节点的访问：

父节点i的左子节点位置2*i+1
父节点i的右子节点位置2*i+2
子节点i的父节点位置floor((i-1)/2)

steps:

根据序列创建最大二叉堆

移除最大二叉堆的根节点（即最大值），重新调整最大二叉堆

动态演示：

c代码：

void shift(int a[],int ind,int n)
{
	int tmp;
	int i = ind;
	int c = i*2+1;

	while (c < n)
	{
		if (c+1<n && a[c] < a[c+1])
		{
			c++;
		}

		if (a[i]>a[c]) 
			break;
		else{
			tmp = a[c];
			a[c] = a[i];
			a[i] = tmp;

			i = c;
			c = 2*i+1;
		}
	}
}

void heap_sort(int a[], int n)
{
	int i,tmp;
	/*初始化堆*/
	for(i=(n-2)/2;i>=0;i--)
		shift(a,i,n);

	for (i=0;i<n;i++)
	{
		/*将堆的根节点保存*/
		tmp = a[0];
		a[0] = a[n-i-1];
		a[n-i-1] = tmp;

		/**/
		shift(a,0,n-i-1);
	}

}   

```   
   
## 基数排序


基数排序是一种**非比较型**的整数排序算法。

[基数排序演示](http://www.cs.usfca.edu/~galles/visualization/RadixSort.html)

原理：
> 将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

steps：
> 1. 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
2. 从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。

(上述时从最右边开始的，称为LSD，Least significant digital，若从最左边开始称为MSD，Most significant digital)

复杂度：
>基数排序的时间复杂度是O(k·n)，其中n是排序元素个数，k是数字位数。注意这不是说这个时间复杂度一定优于O(n·log(n))，k的大小取决于数字位的选择（比如比特位数），和待排序数据所属数据类型的全集的大小；k决定了进行多少轮处理，而n是每轮处理的操作数目。


c代码：

#define MAX 30

#define BASE 10

void radixsort(int array[],int n)
{
int i,b[MAX],exp = 1;
int m = array[0];

/*找出最大数*/
for (i=1;i<n;i++)
{
    if (array[i]>m)
    {
        m = array[i];
    }
}

while(m/exp >0)
{
    int bucket[BASE] = {0};

    /*按位入桶*/
    for(i=0;i<n;i++){
        bucket[(array[i]/exp)%BASE]++;
    }

    for(i=1;i<BASE;i++){
        bucket[i] += bucket[i-1];
    }

    /*根据每位进行一次排序*/
    for (i=n-1;i>=0;i--){
        b[--bucket[(array[i]/exp)%BASE]] = array[i];
    }

    for(i=0;i<n;i++){
        array[i] = b[i];
    }

    exp *= BASE;
}

}

```

排序算法的比较

平均而言，对于一般的随机序列顺序表而言，上述几种排序算法性能从低到高的顺序大致为：

冒泡排序 < 插入排序 < 选择排序 < 希尔排序 < 快速排序

但这个优劣顺序不是绝对的，在不同的情况下，甚至可能出现完全的性能逆转。

对于序列初始状态基本有正序，可选择对有序性较敏感的如:

插入排序、冒泡排序、选择排序等方法

对于序列长度比较大的随机序列，应选择平均时间复杂度较小的快速排序方法。

影响排序效果的因素：

待排序的记录数目n

记录的大小（规模）

关键字的结构及其初始状态

对稳定性的要求

语言工具的条件

存储结构

时间和辅助空间复杂度等

各种排序算法复杂度即稳定性比较

Monkee

Stay Hungry Stay Foolish

排序算法及其比较

冒泡排序

选择排序

插入排序

希尔排序

归并排序

快速排序

堆排序

排序算法的比较

参考：